This tutorial is a high level overview of RPN notation, calculation of constants like π, displaying calculation results, and scaling the calculation to larger sizes.

User input is color highlighted in blue highlighting. The program's response is color highlighted in yellow highlighting.

Navigate to the project folder. To run the program, type: ./calc-pi . Various license and configuration will print. The program will respond with a prompt Op Code: .

~/dev/calc-pi-x86-64-asm$ ./calc-pi 

   (some stuff omitted)

Accuracy: 60 Digits

XREG   0.0
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 0 Seconds 00:00:00) Op Code: 

RPN notation uses a register stack. The stack contains 4 registers X, Y, Z and T. Number input will place the value into the X register. The previous contents are pushed up the stack: X → Y → Z → T. Basic math operations will operate on the bottom of the stack acting on X and Y. The stack is rotated down: Y ← Z ← T.

In this example we will calculate ((4 * 5) / 2). First, the base-10 conversion shall be set to int so interim calculation results will display as integers.

Number input is completed by pressing the keyboard Enter key. Entering 4 will push the value 4 into the X register. Entering 5 will first roll the stack moving 4 from X to Y, then the value of X will be set to 5. You can see the contents of the stack printed after each entry. Math operators like + - * / operate on X and Y registers. Entering * to execute the multiply command multiplying X = X * Y. You can see 20 in X register. Note: the stack rolls down, leaving 0 in Y, Z and T registers. Entering 2 will rotate X to Y leaving 20 in Y, and 2 is placed in the X register. Entering / to call the division routine to calculate Y / X, rolling the stack and leaving 10 in the X register.

(Elapsed time: 0 Seconds 00:00:00) Op Code: int 

XREG   0
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: 4 

XREG  +4 
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: 5 

XREG  +5 
YREG  +4
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: * 

XREG  +20 
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: 2 

XREG  +2 
YREG  +20
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: / 

XREG  +10 
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: 

The program contains a list of sub-programs to calculate math constants. A list can be found here. The command parser can accept text commands between 1 and 7 characters. The command to calculate pi is "c.pi". You will notice program output is still set to "int" mode and the X register still contains "10" from the last example Entering clrall will clear all the calculator registers. Prior to running the calculation, we will configure the variable size to allow 500 digits (base-10) by entering sigfigs 500 . The sub-program to calculate pi can be started by entering c.pi . The result will then be printed by entering print .

XREG  +10
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: clrall

All Varaibles Cleared.

XREG   0 
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: sigfigs 500 

 Accuracy: 500 Digits 

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.pi 

Functon_calc_pi_chud: Calculation of pi using Chudnovsky formula.
Calculation square root 10005

XREG  +3 
YREG   0
ZREG   0
TREG   0

(Elapsed time: 0 Seconds 00:00:00) Op Code: print

 +3 

(Elapsed time: 0s Seconds 00:00:00) Op Code: 

You will notice that the result for π was "3" showing only 1 digit of accuracy. This is because the base-10 converter is still set to integer mode ("int" mode).

All numbers are stored binary floating point format. In order to view the numbers in human understandable output, it is necessary to convert the binary numbers (base-2) to recognizable (base-10) format. The base-10 conversion can be set to 3 modes: fix, int or sci. The program is currently in "int" mode. Change the base-10 conversion to scientific notation by entering sci and then print the result again by entering print command.

(Elapsed time: 0 Seconds 00:00:00) Op Code: sci 


XREG  +3.14159265358979323846264338327950288419716939937510 E+0 
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 0 Seconds 00:00:00) Op Code: print 

+3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865
1328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612
8475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962
8292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051
1854807446237996274956735188575272489122793818301194912 E+0 

(Elapsed time: 0 Seconds 00:00:00) Op Code: 

You will notice the exponent value " E+0" is printed both on the abbreviated stack output and in response to the print command. Next set the base-10 conversion to fix mode by entering fix . We will print the result again, but this time we will use the alternate print command, the period character ".", by entering . to print the result.

(Elapsed time: 0 Seconds 00:00:00) Op Code: fix 


XREG  +3.14159265358979323846264338327950288419716939937510 
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 0 Seconds 00:00:00) Op Code: . 

+3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865
1328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612
8475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962
8292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051
1854807446237996274956735188575272489122793818301194912

(Elapsed time: 0 Seconds 00:00:00) Op Code: 

You will note the exponent has been removed from the output in "fix" mode. In summary, the program is set to internal accuracy of 500 digits. An internal sub-program was executed to calculate the constant π to 500 digits. We printed the result in "fix" notation.

In the previous example, the text output containing the number was a long string of number characters. When it reached the right side of my console window, the text wrapped to the next line. A smaller window would print something like this, however, it is still one single line of text 500 characters long.

+3.14159265358979323846264338327950288419716939937
51058209749445923078164062862089986280348253421170
67982148086513282306647093844609550582231725359408
12848111745028410270193852110555964462294895493038
19644288109756659334461284756482337867831652712019
09145648566923460348610454326648213393607260249141
27372458700660631558817488152092096282925409171536
43678925903600113305305488204665213841469519415116
09433057270365759591953092186117381932611793105118
54807446237996274956735188575272489122793818301194
912

The print command will accept a modifier. The letter "f" will specify text format with number characters in groups of 10 characters separated by a space. These will be set in lines of 100 characters, and for larger numbers, in blocks of 1000 characters. Repeat the print command using the period character, but append "f" by entering . f to print formatted output.

(Elapsed time: 0 Seconds 00:00:00) Op Code: . f 

+3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
   8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
   4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
   7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
   3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912

(Elapsed time: 0 Seconds 00:00:00) Op Code: 

You will probably notice that calculation of π was very fast when the accuracy is limited to 500 digits. In order to increase the accuracy, two factors come into play: memory and time. The size of the variables in terms of number of bytes or number of 64 bit words will need to be increased. The arithmetic part of the program will take more time perform the math operations, in particular long division. The type of arithmetic performed in this program involves basic binary math such as multiplication and long division by rotation of binary bits left and right while subtracting or adding numbers. As variables get larger in size, the time needed for this type of arithmetic scales exponentially. Yes, this implies there is a practical upper limit. In the case of this program, the time limit is reached long before the memory limit.

Calculations can be scaled by trial and error. The accuracy can be increased in steps. The scale factor can be plotted in a spreadsheet by creating a "log-log" chart with the logarithm of the number of digits on the X axis and logarithm of the time in seconds on the Y axis. Here is an example of such a chart made in 2015 when I was first writing the program.

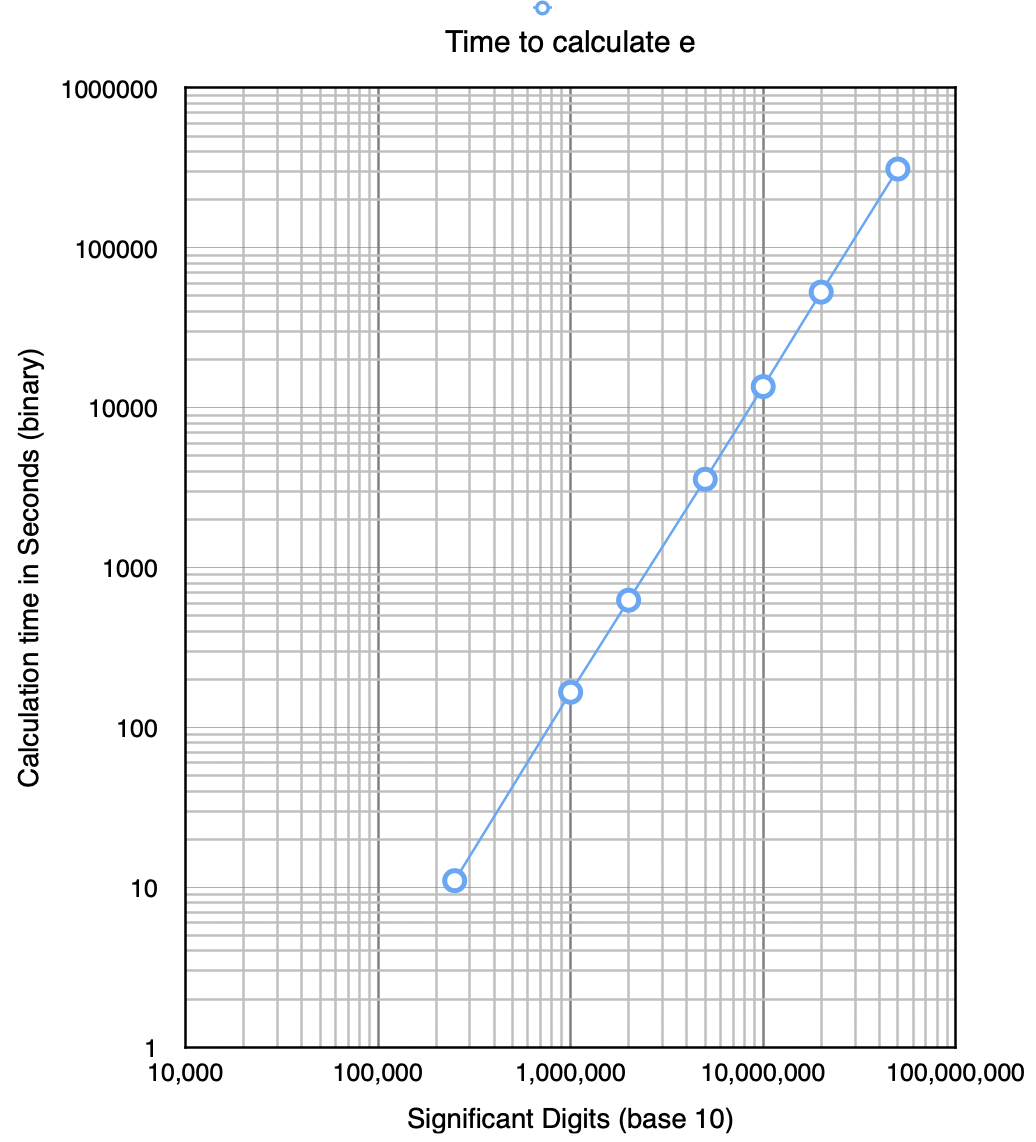
Let's try it. This time we will calculate the constant e with the command "c.e". As seen above, we use clrall to clear previous data. Using the abbreviated version of the "sigfigs" command "sf", we will start with 10000 digits and work our way up.

Enter sf 10000 and then enter c.e .
Enter sf 100000 and then enter c.e .
Enter sf 200000 and then enter c.e .
Enter sf 500000 and then enter c.e .
Enter sf 1000000 and then enter c.e .

Please observe the time needed for the calculation at each step. You will see the time increase exponentially.

(Elapsed time: 0 Seconds 00:00:00) Op Code: clrall 

 All Varaibles Cleared. 

XREG   0.0
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 0 Seconds 00:00:00) Op Code: sf 10000 

Accuracy: 10000 Digits

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 0 Seconds 00:00:00 ) Op Code: sf 100000 

Accuracy: 100000 Digits

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG  +2.71828182845904523536028747135266249775724709369995 E+0
ZREG   0.0
TREG   0.0

(Elapsed time: 2 Seconds 00:00:02 ) Op Code: sf 200000 

Accuracy: 200000 Digits

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG  +2.71828182845904523536028747135266249775724709369995 E+0
ZREG  +2.71828182845904523536028747135266249775724709369995 E+0
TREG   0.0

(Elapsed time: 6 Seconds 00:00:06 ) Op Code: sf 500000 

Accuracy: 500000 Digits

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG  +2.71828182845904523536028747135266249775724709369995 E+0
ZREG  +2.71828182845904523536028747135266249775724709369995 E+0
TREG  +2.71828182845904523536028747135266249775724709369995 E+0

(Elapsed time: 35 Seconds 00:00:35 ) Op Code: sf 1000000 

Accuracy: 1000000 Digits

(Elapsed time: 0 Seconds 00:00:00) Op Code:  c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG  +2.71828182845904523536028747135266249775724709369995 E+0
ZREG  +2.71828182845904523536028747135266249775724709369995 E+0
TREG  +2.71828182845904523536028747135266249775724709369995 E+0

(Elapsed time: 133 Seconds 00:02:13 ) Op Code:

Here we are up to 1 million digits and the time for the calculation of e is 2 minutes 13 seconds. Next, lets check how much memory we are using. The "v" modifier can be added to the sigfigs or sf command to show more verbose information on the size of the variables. Please input sf v to see this.

(Elapsed time: 133 Seconds 00:02:13) Op Code: sf v 


Decimal (base 10) Accuracy:
  Printed Digits:    1000000  (Configurable)
  Extended Digits:   0        (Shows extra digits)
  Useable Digits:    1000016  (Theoretical)
  Total Calc Digits: 1000093  (With Guard Words)
  Available Digits:  40403465 (Useable digits)

Binary Accuracy:
  Mantissa Words: 51906 Words     415248 Bytes
  Guard Words:    4 Words         32 Bytes
  Total Words:    51910 Words     415280 Bytes 
  Exponent Size:  1 Words         8 Bytes
  Available Size: 2097152 Words   16777216 Bytes 

(Elapsed time: 0 Seconds 00:00:00) Op Code:

You can see the program was compiled with about 16 MB allocated to each variable. At 1,000,000 digits, each variable is using about 4 MB of the maximum variable size, so we are using about 1/4 of the memory. Of course, the program can be recompiled with larger variables if you like.

Imagine you are trying a calculation that may take several days to complete. You start the program. You are waiting... and waiting... It would be nice to see some work in progress.

In the case of calculation of e, the terms added to the infinite series get smaller as the calculation progresses. In this case, I have a feature that can sample 4 bit nibbles across equally spaced parts of the mantissa and print the mantissa nibbles using a term counter. In the case of this example, we use the "sstep" command to set the step counter to show every 5000 steps with the command sstep 5000 . The "show" and "showoff" commands will turn on and off the progress bar. Enter show to enable the progress bar. Then repeat the calculation by entering c.e .

(Elapsed time: 0 Seconds 00:00:00) Op Code: sstep 5000 

[iShowCalcStep] = 5000

(Elapsed time: 0 Seconds 00:00:00) Op Code: show 

Show Progress: On, Step = 5000

(Elapsed time: 0 Seconds 00:00:00) Op Code: c.e 

Function_calc_e_Fix: Calculating e using sum 1/n!

Calculation Status variables initialized.

...............|...............| <-- Ruler.
0C532D8C67D63C9CC89F0643369C1345   5000 00:00:06 00:00:06 Shift: 848  No_Word: 51910
00441987DADC52285CEE932EA00F9C55   10000 00:00:12 00:00:06  Shift: 1851  No_Word: 51910
009A1557FB5BD194A226FFA4AF594F49   15000 00:00:18 00:00:06  Shift: 2914  No_Word: 51910
00054E4FF7AE069FEAF932E19A2B79DC   20000 00:00:24 00:00:06  Shift: 4014  No_Word: 51910
0000A9F691F97ED5E988BB10BE6BC9F2   25000 00:00:29 00:00:05  Shift: 5144  No_Word: 51910
00008785D60E30ADEF7DD56F3893133A   30000 00:00:35 00:00:06  Shift: 6296  No_Word: 51910
00000DE316D92D948520CAA9F1A10D49   35000 00:00:40 00:00:05  Shift: 7467  No_Word: 51910
0000006808ECC531011680770B7E9CD9   40000 00:00:45 00:00:05  Shift: 8654  No_Word: 51910
00000002047C885A847B57A09D73E033   45000 00:00:50 00:00:05  Shift: 9855  No_Word: 51910
000000092EB8E4352E8BC5550F073F55   50000 00:00:55 00:00:05  Shift: 11068  No_Word: 51910
0000000028BFA13F6F511450133BF981   55000 00:01:00 00:00:05  Shift: 12293  No_Word: 51910
000000000B58EF2DABD794800D788673   60000 00:01:04 00:00:04  Shift: 13529  No_Word: 51910
000000000051D58775F56705E6155EA4   65000 00:01:09 00:00:05  Shift: 14773  No_Word: 51910
00000000002CA65018FC3D49910AE69E   70000 00:01:13 00:00:04  Shift: 16026  No_Word: 51910
00000000000ECAD68EDAE5C601D62591   75000 00:01:17 00:00:04  Shift: 17288  No_Word: 51910
000000000000DC9EB6D25EA33ECB6B34   80000 00:01:21 00:00:04  Shift: 18557  No_Word: 51910
00000000000007049DB3954316E2E9BA   85000 00:01:25 00:00:04  Shift: 19833  No_Word: 51910
00000000000000D02D2613CA5BB4A3ED   90000 00:01:29 00:00:04  Shift: 21115  No_Word: 51910
00000000000000F4FCC36CEA174B6EEA   95000 00:01:32 00:00:03  Shift: 22404  No_Word: 51910
0000000000000000762108F11193998A   100000 00:01:36 00:00:04 Shift: 23699  No_Word: 51910
00000000000000009585596BC0CC62F9   105000 00:01:39 00:00:03 Shift: 24999  No_Word: 51910
0000000000000000012014D76099883F   110000 00:01:42 00:00:03  Shift: 26305  No_Word: 51910
0000000000000000009CA52C34BDB2D2   115000 00:01:45 00:00:03  Shift: 27616  No_Word: 51910
0000000000000000005400FCB46D5AB3   120000 00:01:48 00:00:03  Shift: 28932  No_Word: 51910
0000000000000000000A6138292A5B0C   125000 00:01:50 00:00:02  Shift: 30252  No_Word: 51910
00000000000000000000E861CF7E3E0F   130000 00:01:53 00:00:03  Shift: 31577  No_Word: 51910
00000000000000000000089ED4851E5B   135000 00:01:55 00:00:02  Shift: 32906  No_Word: 51910
000000000000000000000098A323DE99   140000 00:01:57 00:00:02  Shift: 34240  No_Word: 51910
0000000000000000000000AD363FEFE0   145000 00:01:59 00:00:02  Shift: 35577  No_Word: 51910
000000000000000000000008449922B6   150000 00:02:01 00:00:02  Shift: 36919  No_Word: 51910
0000000000000000000000001935C50D   155000 00:02:03 00:00:02  Shift: 38264  No_Word: 51910
0000000000000000000000000C520981   160000 00:02:04 00:00:01  Shift: 39613  No_Word: 51910
00000000000000000000000000CBF48A   165000 00:02:06 00:00:02  Shift: 40965  No_Word: 51910
0000000000000000000000000006E9CE   170000 00:02:07 00:00:01  Shift: 42321  No_Word: 51910
00000000000000000000000000068D2F   175000 00:02:08 00:00:01  Shift: 43680  No_Word: 51910
000000000000000000000000000057B2   180000 00:02:09 00:00:01  Shift: 45042  No_Word: 51910
0000000000000000000000000000095F   185000 00:02:09 00:00:00  Shift: 46408  No_Word: 51910
00000000000000000000000000000073   190000 00:02:10 00:00:01  Shift: 47776  No_Word: 51910
00000000000000000000000000000006   195000 00:02:10 00:00:00  Shift: 49148  No_Word: 51910
00000000000000000000000000000000   200000 00:02:11 00:00:01  Shift: 50522  No_Word: 51910
00000000000000000000000000000000   205000 00:02:11 00:00:00 Shift: 51899  No_Word: 51910

 iCounter01=205038  Command: 00:02:11  Shift:  No_Word:

XREG  +2.71828182845904523536028747135266249775724709369995 E+0
YREG   0.0
ZREG   0.0
TREG   0.0

(Elapsed time: 131 Seconds 00:02:11) Op Code:

Notice two things. First, the time needed for each set of 5000 terms decreases starting at 6 seconds per 5000 terms, decreasing to less than 1 second per 5000 terms added to the infinite sum. Second, the "shift" number shows the number of words the mantissa must be shifted to add next term to the series sum. As the shift count approaches the word count, the accuracy of the factorial 1/n term may be decreased.

The progress bar functions must be embedded manually into a given infinite series. Therefore, not all calculations show the progress bar.

Well, there you have it. You just calculated the constant e to 1 million decimal places. You can print it with . f and watch it scroll past. I'll stop here and leave that part to you. Have fun exploring numbers.