| Command | Input | Output | Description |
|---|---|---|---|
| c.pi | Xreg |
Calculates pi using default method Default is Chudnovsky formula |
|
| c.pi.ch | Xreg | Calculates pi using Chudnovsky formula | |
| c.pi.ra | Xreg | Calculates pi using Ramanujan formula | |
| c.pi.st c.pi.st <a> |
Xreg |
Calculates pi using Størmer formula. Appending 1,2,3, or 4 as an argument will break up the calculation into 4 parts. This will allow 4 instances of the program to be run concurrently 1 - Output to file "pi-st-1.num" 2 - Output to file "pi-st-2.num" 3 - Output to file "pi-st-3.num" 4 - Output to file "pi-st-4.num" 1234 - Combine all 4 files." |
Low Precision π (pi) functions
| Command | Input | Output | Description |
|---|---|---|---|
| c.pi.ze | Xreg |
Estimate pi using the formula: zeta(2) = (π2)/6 |
|
| c.pi.mc | Xreg | Estimate pi using a Monte Carlo simulation. |
Some other Constants
| Command | Input | Output | Description |
|---|---|---|---|
| c.e c.e <a> |
Xreg |
"c.e" calculates e by default method. Appending 1,2,3, or 4 as an argument will select between several different methods. 1 - Sum 1/n in fixed precision 2 - Sum 1/n i7 Register (64 bit DIV) 3 - Full floating point arithmetic 4 - Use f.exp function f.exp with Xreg=1 |
|
| c.gr | Xreg | Calculates Golden Ratio | |
| c.ln2 | Xreg | Calculates natural log of 2. ln(2) | |
| c.sr2 | Xreg |
Square root of 2 |
The following is a quick overview of several methods to calculate pi that are used in this program. If you would like to know more about π, Wikipedia has a great page here.
The Chudnovsky formula is my favorite method to calculate pi. You can read more about it on Wikipedia here. This is rapidly convergent. This program adds 711 terms of the infinite series to calculate 10,000 digits, which is about 14 digits per term. You may notice a delay at the start of the program, because the square root sqrt(10005) is calculated before starting the infinite series summation.

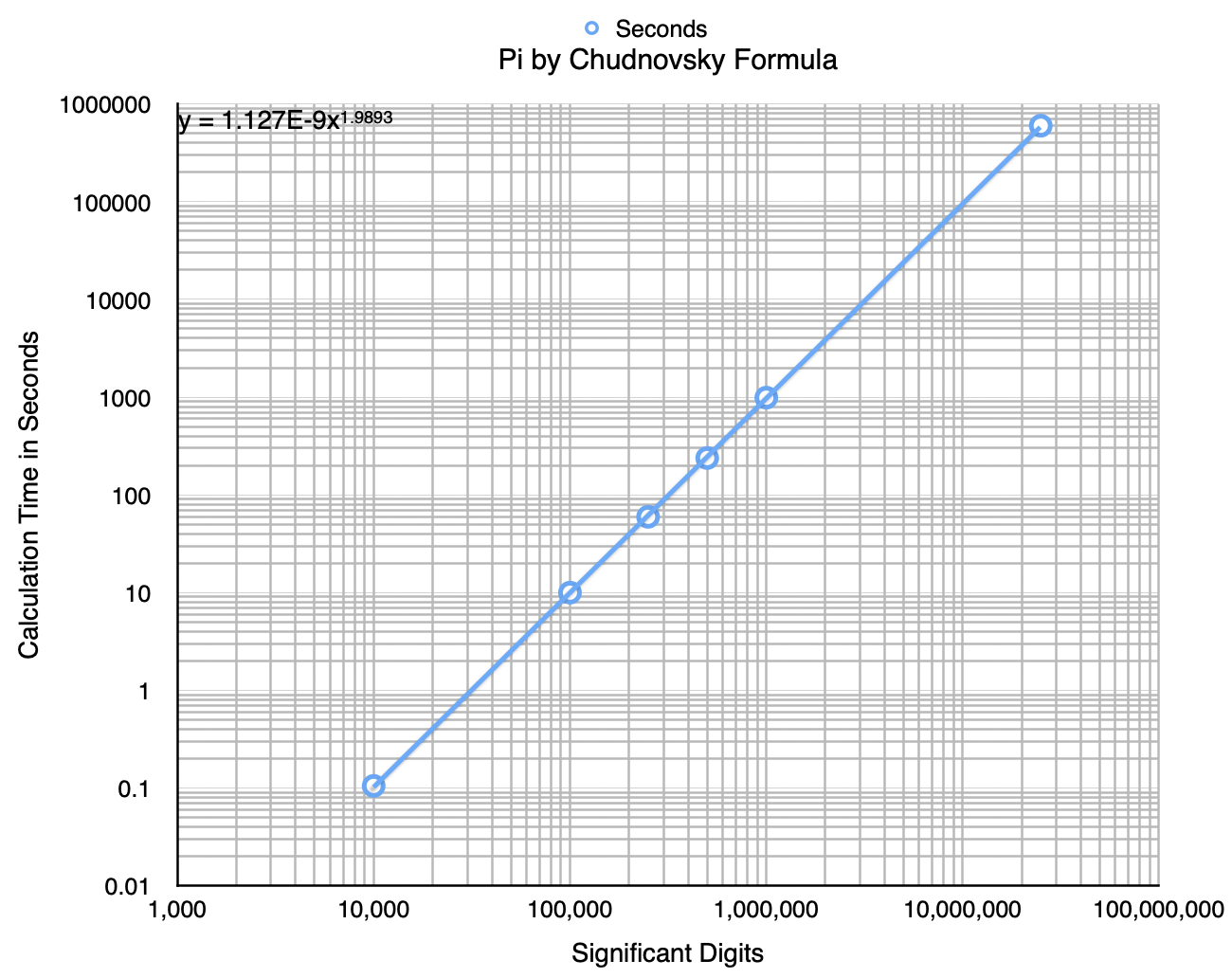
This is a chart made in 2015 showing the time to calculate π using the Chudnovsky formula. The line shows how this type of arithmetic scales (or perhaps does not scale) to larger size. It was run a Dell XPS with an i7-4790 processor that I bought in 2014. This does not include the base-10 conversion.
Ramanujan is a famous Indian mathematician. Over 100 year ago, he came up with this formula for pi. This program adds 1264 terms of the infinite series to calculate 10,000 digits, which is just under 8 digits per term.
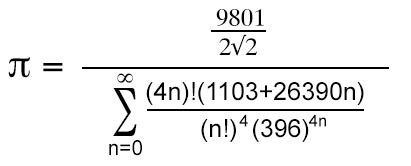
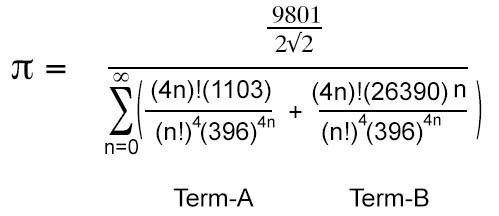
With a little simple algebra, the Ramanujan formula can be rearranged to allow a more efficient calculation. Calculation in this program use this form.
There are two variations to the implementation of the Størmer formula in this program. You can use "c.pi.st" to calculate π using the formula below.
The other method involves calculation of each of the 4 terms of the formula independently. Computers with a quad core processor can run 4 copies of the calc-pi program at the same time. Commands "c.pi.st 1", "c,pi-st 2", "c.pi-st 3", and "c.pi-st 4" will calculate each of 4 parts separately and save the results into separate disk files. The command "c.pi.st 1234" will read all 4 parts from the disk and combine them.
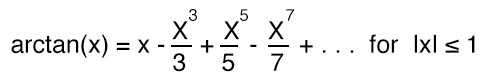
This is an interesting case, but perhaps not a very efficient way to calculate pi.
This series converges extremely slowly. It will only produce a few digits of π, but it is interesting to see how it works and how slowly it converges.
To perform the calculation, set accuracy to 10 with input "sigfigs 10".
Set the number of cycles with the "slimit" function by typing "slimit 1000000". (or other value)
Next calculate the series with "c.pi.ze".
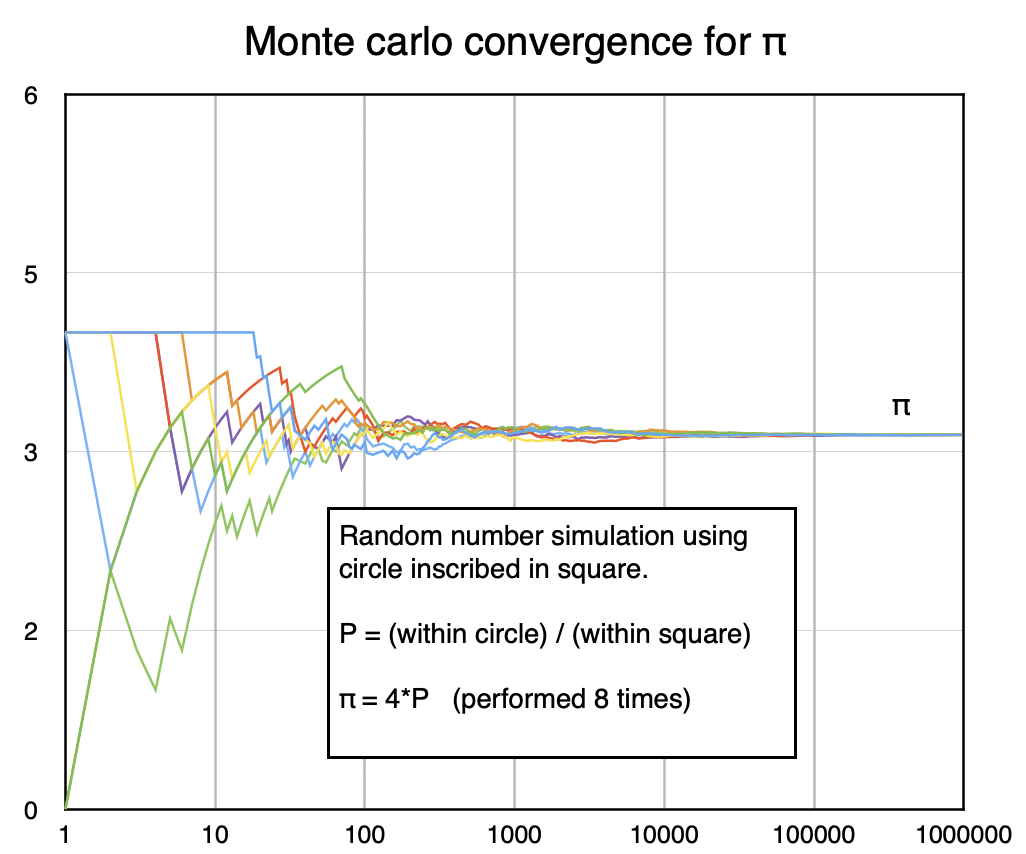
It is possible to estimate the value of π using a random number generator. Take a unit circle of radius R = 1. Circumscribe a square around it with sides of the square length 2. The area of the circle is A = π * R2. Since R = 1, the area of circle is A = π. The area of the circulscribed square is A = 2 * 2 = 4.
Next take a random number generator and generate a series of random X,Y values in the range of -1 < X < 1 and -1 < Y < 1. Using the formula for a right triangle, the radius of the point at (X,Y) is R = sqrt(X2 + Y2). In the case R < 1, the point is inside the circle. In the case R > 0, the point is outside the circle. Since the ratio of area of the square (4) to the area of the circle (π). We can count the points inside the circle and points outside the circle. The ratio of the counts inside verses outside can be used to calculate the value of π. This is known as a Monte Carlo simulation because it "rolls the dice" each time to see where the point would be.
To perform the calculation, set accuracy to 10 with input "sigfigs 10".
Set the number of cycles with the "slimit" function by typing "slimit 1000000". (or other value)
Next run the Monte Carlo by typing "c.pi.mc".
The random number source is the assembly language RDRAND command to use the i7 microprocessor RNG. Each time the program is run, the number will be slightly different. Note, it is not very accurate compared to the other methods.