This tutorial is a high level overview of RPN notation, calculation of constants like π, displaying calculation results, and scaling the calculation to larger sizes.

User input is color highlighted in blue highlighting. The program's response is color highlighted in yellow highlighting.

If you have not done so already, follow the instructions in the README.md file to clone the GitHub repository. Then navigate to the src folder in the project folder. Use the make command to compile the program using instructions in the README.md file.

Navigate to the project folder. Navigate to the "src" in the project folder To run the program, type: ./calc-pi . Various license and configuration will print. The program will respond with a prompt Op Code: .

  ~/asm/calc-pi-arm64-asm/src $ ./calc-pi 

     (some license text omitted)

Calculation of Pi on Raspberry Pi
Written in GNU Assembler (as)
Assembled arch=armv8-a cpu=cortex-a72
     
I/O Initialized

Accuracy: 60 Digits (fraction part)

Variables initialized.

  (Elapsed: 0.040 Sec) Op Code:

RPN notation uses a register stack. The stack contains 4 registers X, Y, Z and T. Number input will place the value into the X register. The previous contents are pushed up the stack: X → Y → Z → T. Basic math operations will operate on the bottom of the stack acting on X and Y. The stack is rotated down: Y ← Z ← T.

In this example we will calculate ((4 * 5) / 2).

After each operation, if the result is other than zero, the first 50 decimal places will be shows as a calculation preview.

Number input is completed by pressing the keyboard Enter key. Entering 4 will push the value 4 into the X register. Entering 5 will first roll the stack moving 4 from X to Y, then the value of X will be set to 5. You can see the contents of the stack printed after each entry. Math operators like + - * / operate on X and Y registers. Entering * to execute the multiply command multiplying X = X * Y. You can see 20 in X register. Note: the stack rolls down, leaving 0 in Y, Z and T registers. Entering 2 will rotate X to Y leaving 20 in Y, and 2 is placed in the X register. Entering / to call the division routine to calculate Y / X, rolling the stack and leaving 10 in the X register.

  (Elapsed: 0.046 Sec) Op Code: 4 

XREG   +4.00000000000000000000000000000000000000000000000000 
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.004 Sec) Op Code: 5 

XREG   +5.00000000000000000000000000000000000000000000000000 
YREG   +4.00000000000000000000000000000000000000000000000000
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.005 Sec) Op Code: * 

XREG   +20.00000000000000000000000000000000000000000000000000 
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.010 Sec) Op Code: 2 

XREG   +2.00000000000000000000000000000000000000000000000000 
YREG   +20.00000000000000000000000000000000000000000000000000
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.007 Sec) Op Code: / 

XREG   +10.00000000000000000000000000000000000000000000000000 
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.003 Sec) Op Code:

The program contains a list of sub-programs to calculate math constants. A list can be found here. The command to calculate pi is "c.pi". Entering clrstk will clear the stack, which are calculator registers X, Y, Z and T. Prior to running the calculation, we will configure the variable size to allow 500 digits (base-10) by entering sigfigs 500 . The sub-program to calculate pi can be started by entering c.pi . The result will then be printed by entering print . The program will print 500 digits without formatting, so each line of the number will wrap, depending on the width of the terminal.

XREG   +10.00000000000000000000000000000000000000000000000000
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.004 Sec) Op Code: clrstk 

XREG   +0.0 
YREG   +0.0 
ZREG   +0.0 
TREG   +0.0 

  (Elapsed: 0.002 Sec) Op Code: sigfigs 500 

 Accuracy: 500 Digits (fraction part) 

  (Elapsed: 0.002 Sec) Op Code: c.pi 

 Calculating: Square Root 10005  (Elapsed: 0.005 Sec) 
 Calculating: Chudnovsky infinite series  (Elapsed: 0.010 Sec) 

XREG   +3.14159265358979323846264338327950288419716939937510 
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.014 Sec) Op Code: print 

 +3.1415926535897932384626433832795028841971693993751058209749
 4459230781640628620899862803482534211706798214808651328230664
 7093844609550582231725359408128481117450284102701938521105559
 6446229489549303819644288109756659334461284756482337867831652
 7120190914564856692346034861045432664821339360726024914127372
 4587006606315588174881520920962829254091715364367892590360011
 3305305488204665213841469519415116094330572703657595919530921
 8611738193261179310511854807446237996274956735188575272489122
 793818301194912(9833673362) 

  (Elapsed: 0.017 Sec) Op Code:

In the previous example, the text output containing the number was a long string of number characters. When it reached the right side of my console window, the text wrapped to the next line. A smaller window would print something like this, however, it is still one single line of text 500 characters long.

+3.14159265358979323846264338327950288419716939937
51058209749445923078164062862089986280348253421170
67982148086513282306647093844609550582231725359408
12848111745028410270193852110555964462294895493038
19644288109756659334461284756482337867831652712019
09145648566923460348610454326648213393607260249141
27372458700660631558817488152092096282925409171536
43678925903600113305305488204665213841469519415116
09433057270365759591953092186117381932611793105118
54807446237996274956735188575272489122793818301194
912

The print command will accept a modifier. The letter "f" will specify text format with number characters in groups of 10 characters separated by a space. These will be set in lines of 100 characters, and for larger numbers, in blocks of 1000 characters. Repeat the print command using the period character, but append "f" by entering . f to print formatted output.

  (Elapsed: 0.017 Sec) Op Code: . f 

 +3.
  1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 
  8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 
  4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 
  7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 
  3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
 (9833673362 ) 

  (Elapsed: 0.008 Sec) Op Code:

You will probably notice that calculation of π was very fast when the accuracy is limited to 500 digits. In order to increase the accuracy, two factors come into play: memory and time. The size of the variables in terms of number of bytes or number of 64 bit words will need to be increased. The arithmetic part of the program will take more time perform the math operations, in particular long division. The type of arithmetic performed in this program involves basic binary math such as multiplication and long division by rotation of binary bits left and right while subtracting or adding numbers. As variables get larger in size, the time needed for this type of arithmetic scales exponentially. Yes, this implies there is a practical upper limit. In the case of this program, the time limit is reached long before the memory limit.

Calculations can be scaled by trial and error. The accuracy can be increased in steps. The scale factor can be plotted in a spreadsheet by creating a "log-log" chart with the logarithm of the number of digits on the X axis and logarithm of the time in seconds on the Y axis. This is what a Raspberry Pi 3B would look like using this program to calculate e.

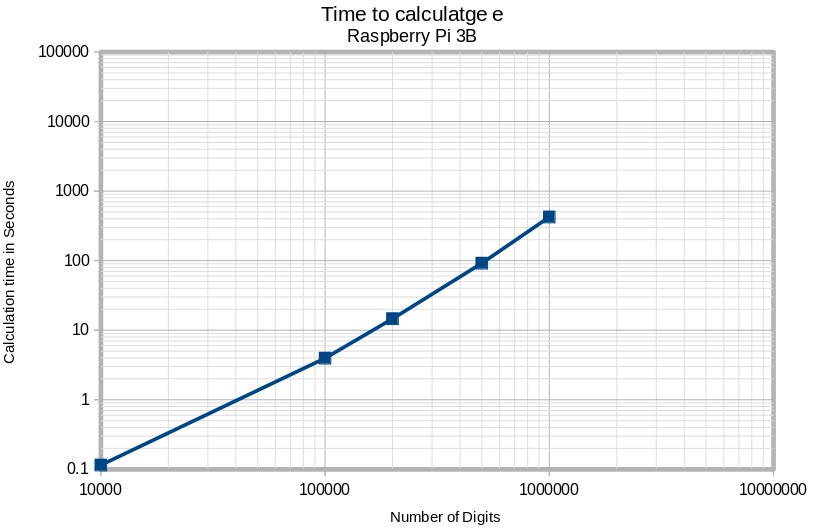
Let's try it. This time we will calculate the constant e with the command "c.e". As seen above, we use clrstk to clear previous data. Using the abbreviated version of the "sigfigs" command "sf", we will start with 10000 digits and work our way up.

Enter sf 10000 and then enter c.e .
Enter sf 100000 and then enter c.e .
Enter sf 200000 and then enter c.e .
Enter sf 500000 and then enter c.e .
Enter sf 1000000 and then enter c.e .

Please observe the time needed for the calculation at each step. You will see the time increase exponentially.

  (Elapsed: 0.046 Sec) Op Code: clrstk 

XREG   +0.0
YREG   +0.0
ZREG   +0.0
TREG   +0.0

  (Elapsed: 0.002 Sec) Op Code: sf 10000 

Accuracy: 10000 Digits (fraction part)

  (Elapsed: 0.001 Sec) Op Code: c.e 

Function_calc_e: Calculating e using sum 1/n!

XREG   +2.71828182845904523536028747135266249775724709369995
YREG   +3276.00000000000000000000000000000000000000000000000000
ZREG   +0.0
TREG   +0.0

   (Elapsed: 0.115 Sec) Code: sf 100000 

Accuracy: 100000 (fraction part)

  (Elapsed: 0.001 Sec) Op Code: c.e 

Function_calc_e: Calculating e using sum 1/n!

XREG   +2.71828182845904523536028747135266249775724709369995
YREG   +25226.00000000000000000000000000000000000000000000000000
ZREG   +2.71828182845904523536028747135266249775724709369995
TREG   +3276.00000000000000000000000000000000000000000000000000

   (Elapsed: 3.957 Sec) Op Code: sf 200000 

Accuracy:200000 Digits (fraction part)

  (Elapsed: 0.000 Sec) Op Code: c.e 

Function_calc_e: Calculating e using sum 1/n!

XREG   +2.71828182845904523536028747135266249775724709369995
YREG   +47197.00000000000000000000000000000000000000000000000000
ZREG   +2.71828182845904523536028747135266249775724709369995
TREG   +25226.00000000000000000000000000000000000000000000000000

   (Elapsed: 14.609 Sec) Op Code: sf 500000 

Accuracy: 500000 Digits (fraction part)

  (Elapsed: 0.000 Sec) Op Code: c.e 

Function_calc_e: Calculating e using sum 1/n!

XREG   +2.71828182845904523536028747135266249775724709369995
YREG   +108671.00000000000000000000000000000000000000000000000000
ZREG   +2.71828182845904523536028747135266249775724709369995
TREG   +47197.00000000000000000000000000000000000000000000000000

   (Elapsed: 91.922 Sec) Op Code: sf 1000000 

Accuracy: 1000000 Digits (fraction part)

  (Elapsed: 0.001 Sec) Op Code: c.e 

Function_calc_e: Calculating e using sum 1/n!

XREG   +2.71828182845904523536028747135266249775724709369995
YREG   +205040.00000000000000000000000000000000000000000000000000
ZREG   +2.71828182845904523536028747135266249775724709369995
TREG   +108671.00000000000000000000000000000000000000000000000000

   (Elapsed: 423.877 Sec) Op Code: 

Here we are up to 1 million digits and the time for the calculation of e is 7 minutes 3 seconds. Next, lets check how much memory we are using. The "v" modifier can be added to the sigfigs or sf command to show more verbose information on the size of the variables. Please input sf v to see this. Reminder, the word size is 8 bytes. Each word represents approximately 19.266 decimal digits (base 10).

  (Elapsed: 423.877 Sec) Op Code: sf v 

Printed digits
  Integer part:        [From number]
  Fraction part:       1000000  Digits
  Extended:            10       Digits

Decimal (base 10) Accuracy:
  Max Integer Part     37       Digits
  Fraction Part:       1000015  Digits
  Guard Words:         76       Digits
  Calculation:         1000131  Digits
  Max Fraction Part:   5050367  Digits

Binary (64 bit word) Accuracy:
  Integer Part:        2        Words
  Fraction Part:       51906    Words
  Guard Words:         4        Words
  Combined:            51912    Words
  Available:           262146   Words

  (Elapsed: 0.019 Sec) Op Code: 

You can see the program was compiled with about 2.1 MB allocated to each variable. At 1,000,000 digits, each variable is using about 0.4 MB of the maximum variable size, so we are using about 20% of the declared memory. Of course, the program can be recompiled with larger variables if you like.

Well, there you have it. You just calculated the constant e to 1 million decimal places. You can print it with . f and watch it scroll past. I'll stop here and leave that part to you. Have fun exploring numbers.