| Command | Input | Output | Description |
|---|---|---|---|
| c.pi | Xreg |
Calculates pi using default method Default is Chudnovsky formula |
|
| c.pi.ch | Xreg | Calculates pi using Chudnovsky formula |
Some other Constants
| Command | Input | Output | Description |
|---|---|---|---|
| c.e c.e <a> |
Xreg |
"c.e" calculates e by Sum 1/n! in fixed precision |
Functions Constants
| Command | Input | Output | Description |
|---|---|---|---|
| sqrt | Xreg | Xreg |
Calculate the square root of XReg. Stack not rotated after sqrt(XReg) |
The following is a quick overview of one method to calculate pi that is used in this program. If you would like to know more about π, Wikipedia has a great page here.
The Chudnovsky formula is my favorite method to calculate pi. You can read more about it on Wikipedia here. This is rapidly convergent. This program adds 711 terms of the infinite series to calculate 10,000 digits, which is about 14 digits per term. You may notice a delay at the start of the program, because the square root sqrt(10005) is calculated before starting the infinite series summation.

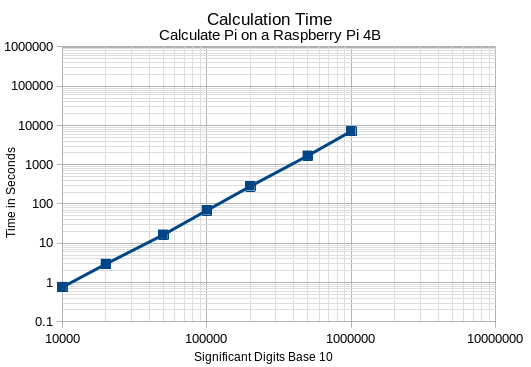
This is a chart made in 2021 showing the time to calculate π using the Chudnovsky formula. The line shows how this type of arithmetic scales (or perhaps does not scale) to larger size. It was run on a Raspberry Pi 4B. This does not include the base-10 conversion.